머신러닝 모델 중 서포트벡터머신(SVM - Support Vector Machine)이 무엇인지 알아보고,어떻게 동작하는지, Maximum Margin과 Soft Margin 의 차이는 무엇인지 알아보겠습니다. 또한 서포트벡터머신의 커널 트릭과 사이킷런(Scikit-learn) 라이브러리를 이용한 코드 예제도 함께 살펴보겠습니다.

서포트벡터머신 모델이란?
서포트벡터머신(Support Vector Machine, SVM) 모델은 linear 또는 nonlinear classification, regression, outlier detection 등에 쓰이는 강력하고 다재다능한 머신러닝 모델입니다. 그렇기 때문에 가장 널리 사용되는 모델들 중 하나입니다. 서포트벡터머신의 목표는 N차원에 분포한 서로다른 데이터 그룹을 나누는 초평면(hyperplane)을 찾는 것입니다. 이 말만 들어서는 이해가 잘 안되실텐데요. 서포트벡터머신 모델이 동작하는 방식을 이해하기 위해 필요한 개념들을 차근차근 소개해드리겠습니다. 이 모델을 공부하기전 Linear Regression과 Logistic Regression을 이해하고 보면 더욱 좋습니다.
Maximum Margin Classification
Maximum Margin Classification에 대한 개념을 이해하기 쉽게 Iris Data에 비추어 설명드리겠습니다. 다음과 같이 Vesicolor라는 종과 Setosa라는 서로 다른 아이리스 꽃 종은 Petal Width와 Petal length 분포에서 크게 차이를 보입니다. 이 두 종을 classification하기 위해서 decision boundary를 그려본다고할 때, 두 데이터 그룹 사이를 나누는 선을 그리는 방법은 많이 있겠지만, 서로의 class 사이의 폭(margin)을 가장 크게 나누도록 그리는 것을 Maximum Margin Classification이라고 합니다. 서로 다른 그룹의 데이터들이 나눠지기 쉽게 잘 분포되어있다면 이 Maximum Margin Classifier를 이용하여 Classification하는게 가장 좋겠지만, 만약 Outlier가 많이 섞인 노이즈가 많은 데이터들이라면, 이 방법을 사용하면 margin이 굉장히 좁게 형성될 것입니다. 이를 보완하기 위한 것이 아래에서 설명드릴 Soft Margin Classification입니다.

Soft Margin Classification
Soft Margin Classification는 약간의 misclassification을 감수하고서라도 좀 더 일반화된 Decision Boundary를 찾는 방법입니다. 위에서 Outlier가 있을 때 Maximum Margin Classification 방법을 사용하면 Margin이 너무 작게 형성되어 generalization을 제대로 하지 못하는 경우를 보았습니다. 이 때 보완책으로 이 방법을 사용할 수 있습니다. 사이킷런(Scikit-learn)을 사용하여 SVM 모델을 만드는 경우 하이퍼파라미터 설정을 통해 어느정도 misclassification을 허용할 것인지 조절할 수 있습니다.

Support Vector란? (서포트 벡터)
그럼 서포트 벡터 머신에서 '서포트 벡터'가 의미하는 것은 무엇일까요? 서포트 벡터는 위의 예시에서 decision boundary에 가장 가까이 있는 데이터 포인트들을 말합니다. 이들은 Decision Boundary의 위치를 정하는 중요한 역할을 합니다.
Non-Linear Classification Problem
위에서 살펴본 데이터는 linearly separable한 데이터였습니다. 하지만 실생활의 데이터들은 이렇게 쉽게 나눠지지 않는 non-linear한 데이터들이 대부분입니다. 이 경우 서로 다른 그룹의 데이터를 구분하는 hyperplane을 찾는 것은 polynomial(다항식)을 적용하는 것입니다. 아래의 그림과 같이 1차원의 데이터 x1이 있고, linear한 선으로 두그룹의 데이터를 나누기 힘든 non-linear classification이 필요한 상황입니다. 이 경우 이를 2차원의 형태로 변경해서 x2 = (x1)^2로 변환시키면 아래와 같이 linear한 hyperplane을 찾을 수 있습니다.

서포트벡터머신의 커널 트릭(Kernel Trick)
위의 개념을 활용하여 계속해서 고차원으로 데이터를 변환하다보면 non-linear한 데이터들도 classification을 할 수 있지만, 고차원으로 데이터를 변환하고 hyperplane을 찾아가는 것은 복잡한 계산을 요구하는 일입니다. 서포트벡터머신은 이렇게 차원을 증가시키는 것을 일일이 다 계산하지 않고, dot product를 이용하는 커널 트릭(Kernel Trick)을 사용합니다. 커널 트릭은 low dimension의 데이터포인트를 input으로 받고 higher dimension 데이터포인트에 해당하는 output을 내놓습니다. 예시를 들어 살펴보겠습니다.
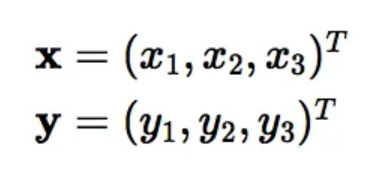
만약 위와 같은 low dimension (3차원) 데이터가 있고 이를 9차원으로 변환하려면 아래와 같은 과정을 거쳐야합니다.
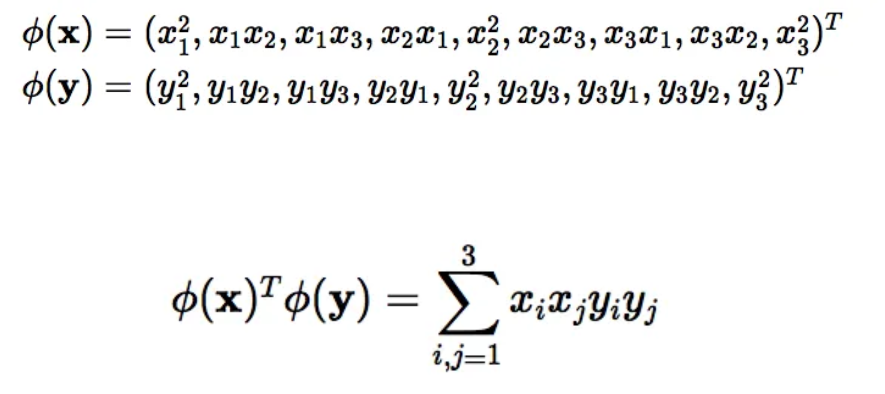
이 과정은 복잡한 계산을 요구합니다. 하지만 이렇게 해서 나온 결과는 아래와 같이 X를 transpose해서 y과 dot product를 구한 결과값과 동일합니다. 커널 트릭은 아래와 같이 dot product를 이용해서 계산을 최소화한 것을 말합니다.
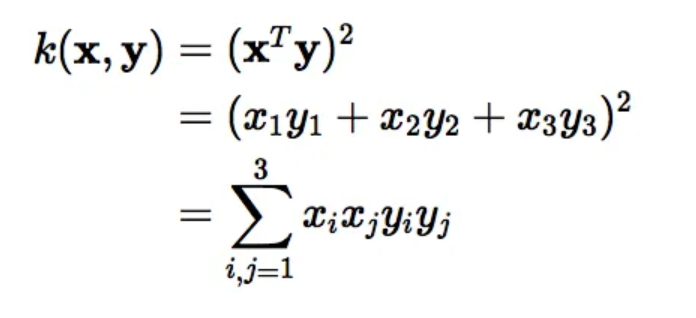
이 커널 트릭을 통해 서포트벡터머신 모델은 빠르게 계산을 할 수 있게 됩니다.
서포트 벡터 머신의 커널 종류는 다음과 같이 여러가지가 있으며, 사이킷런을 이용할 때 하이퍼파라미터로 커널 종류를 설정할 수 있습니다.
- Polynomial Kernel
- Gaussian Kernel
- Radial Basis Function (RBF)
- Laplace RBF Kernel
- Sigmoid Kernel
- Anove RBF Kernel
사이킷런(Scikit-learn)으로 SVM(서포트벡터머신, Support Vector Machine) 머신러닝 코딩해보기
아래 예시는 사이킷런 패키지를 이용하여 아이리스 데이터 Classification 서포트벡터머신 모델을 적용해본 것입니다. 그리고 아래에는 서포트벡터머신 모델이 어떻게 데이터를 나눴는지 Decision Boundary를 plot으로 그려본 예제입니다.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import svm
# Load the iris dataset
iris = datasets.load_iris()
# Take only the first two features for visualization
X = iris.data[:, :2]
y = iris.target
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# Train an SVM model with a radial basis function (RBF) kernel
clf = svm.SVC(kernel='rbf', C=1, gamma='scale')
clf.fit(X_train, y_train)
# Make predictions on the testing set
y_pred = clf.predict(X_test)
# Evaluate the model's performance
accuracy = clf.score(X_test, y_test)
print('Accuracy: {:.2f}'.format(accuracy))# Create a meshgrid of points to plot the decision boundary
xx, yy = np.meshgrid(np.arange(X[:, 0].min() - 0.5, X[:, 0].max() + 0.5, 0.02),
np.arange(X[:, 1].min() - 0.5, X[:, 1].max() + 0.5, 0.02))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the decision boundary
plt.contourf(xx, yy, Z, cmap=plt.cm.Accent, alpha=0.8)
# Plot the training points
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Accent)
# Set the plot limits and labels
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('SVM Classifier with RBF Kernel')
plt.show()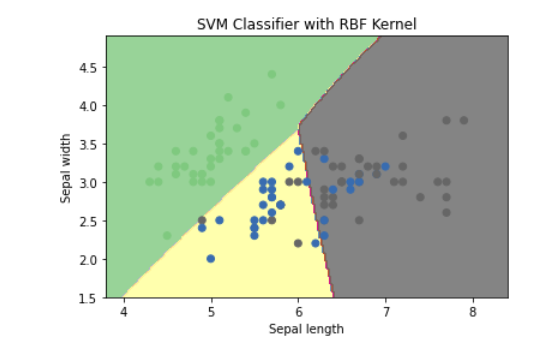
서포트벡터머신은 이렇게 non-linear한 데이터들도 분류할 수 있기 때문에 다양한 상황에 많이 이용되는 모델 중 하나입니다. 서포트벡터머신 모델을 이해하려면 Maximum margin과 Soft margin의 차이를 이해하고, 각각의 장단점은 무엇인지, 사이킷런(Scikit-learn)을 활용하여 코딩을 할 때 각 하이퍼파라미터가 어떤의미를 가지고 어떻게 변화시키면서 이용하는지 이해해야합니다. 오늘 포스팅에서는 서포트벡터머신의 개념과 함께 코드 예제를 같이 살펴보았습니다. Support Vector machine(SVM)을 이해하는 데 도움이 되셨길 바랍니다.
(참고하면 좋을 포스팅)
노코드 머신러닝 툴 WEKA 사용방법(코딩 없이 Machine Learning하기)
코딩을 할 줄 몰라도 머신러닝을 할 수 있는 방법이 있습니다. 잘 만들어진 GUI 툴을 이용하는 것인데요. 데이터만 로드하면 수십가지 머신러닝 모델을 적용해보고 퍼포먼스를 평가해보고 결과
datasciencediary.tistory.com
Classification Decision Tree (결정트리) 개념 - Information gain, impurity, Entropy 이해
Decision Tree(결정트리)는 Classification을 하기 위해 트리를 그려 마지막 leaf node에서 class가 구분되도록 하는 모델이다. Classification이 어떤 방식에 의해 결정이 됐는지 확인하기가 직관적이고 시각화
datasciencediary.tistory.com
'머신러닝' 카테고리의 다른 글
| 머신러닝 ROC curve(커브), AUC 개념 제대로 이해하기 (0) | 2023.02.22 |
|---|---|
| [머신러닝] KNN 알고리즘 (K-Nearest Neighbor) (0) | 2023.02.20 |
| [파이썬 머신러닝] 사이킷런(Scikit-learn) 소개 (0) | 2023.02.18 |
| 노코드 머신러닝 툴 WEKA 사용방법(코딩 없이 Machine Learning하기) (0) | 2023.02.15 |
| Logistic Regression 이해하기 : Sigmoid 함수, ROC 커브, Threshold 찾기 (0) | 2023.02.13 |




댓글