Linear Regression 모델은 Supervised Machine Learning(지도학습)에서 가장 기본적이고 많이 쓰이는 모델입니다. 이 포스팅에서는 기본적인 개념과 Linear Regression의 Cost Function, 이를 최적화하기 위한 Gradient Descent 알고리즘에 대해 알아보겠습니다.
Linear Regression이란
Linear Regression은 우리말로는 선형회귀 모델이라고 불립니다. 이 모델은 여러가지 항목과 우리가 예측하고자하는 타겟 값이 있을 때, 각 변수들과 타겟 값 사이의 관계를 가장 잘 나타내는 선을 통계적으로 찾아내는 모델입니다. 여기서 타겟 값은 continuous한 numerical value이어야하고, 다른 변수들은 continuous한 numerical value이거나, 카테고리 값일 경우 0, 1, ...., 3 과 같이 숫자로 먼저 변환되어야 합니다. Linear Regression을 적용할 수 있는 데이터를 예를 들면, 아파트 가격을 예측하는 모델을 생각해볼 수 있습니다. 방 갯수, 화장실 갯수, 아파트 평수, 역과의 거리, 층수 등의 변수들이 있고 이 변수들과 아파트 가격사이의 관계를 가장 잘 나타내는 함수를 찾아내서 아파트 가격을 예측하는 Linear Regression 모델을 만들 수 있습니다. Linear Regression의 함수는 다음과 같습니다.
Y = b0 + b1 * X1 + b2 * X2 + ... + bn * Xn
Linear Regression의 Cost Function
Linear Regression은 데이터를 가장 잘 나타내는 라인을 찾기위해서 Cost Function이라는 개념을 사용합니다. Cost Function이란 Loss Function이라고도 불리는데요. 예측값과 실제값 사이의 차이를 측정하는 함수입니다. 가장 많이 사용되는 함수는 MSE(Mean Squared Error) function 으로 두 값 사이의 차이를 제곱한 값들의 평균치를 구하는 함수입니다.
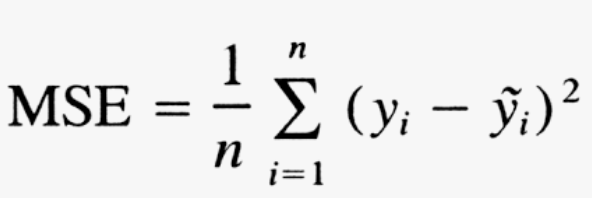
Gradient Descent 알고리즘이란
Gradient Descent 알고리즘은 Cost를 최소화하는 방향으로 Linear Regression모델을 최적화하는 알고리즘입니다. Gradient Descent 알고리즘은 처음에 랜덤 값으로 모든 Coefficient 값을 세팅하고, Cost Function이 적어지는 방향으로 계속해서 Coefficient 값을 업데이트 해나갑니다. 업데이트하는 아래의 식으로 표현될 수 있습니다.
θj = θj - α * ∂/∂θj (J(θ0, θ1, ... , θn))여기서 θj 는 j번째 Coefficient 값을 의미하고 α는 learning rate을 의미합니다. 그리고 J(θ0, θ1, ... , θn)는 cost function을 의미합니다. 그러니까 cost function을 θj로 미분하면 θj로인한 cost function의 변화의 기울기를 의미합니다. 따라서 learning rate α가 작으면 매 반복을 수행할 때마다 굉장히 조금씩 cost function이 줄어드는 방향으로 수렴을 하게 되고 learning rate α가 크면 반대로 굉장히 큰 폭으로 움직이게 됩니다. 따라서 α값을 적당하게 잘 설정하는 것도 Gradient Descent 알고리즘에서는 중요한 부분입니다.
Gradient Descent Algorithm이 하는일 코드 예시로 이해하기
다음은 Gradient Descent Algorithm이 어떤식으로 Cost를 최소화해나가는지 이해를 돕기위핸 코드 예시입니다.
import numpy as np
# generate a sample dataset
np.random.seed(0)
x = np.linspace(0,10,100)
y = 2*x + 1 + np.random.normal(0,1,100)
# initialize the coefficients
theta0 = 0
theta1 = 0
# set the learning rate
alpha = 0.1
# number of iterations
n_iterations = 1000
# perform gradient descent
for i in range(n_iterations):
y_pred = theta0 + theta1*x
error = y - y_pred
cost = (1/2*len(x)) * np.sum(error**2)
theta0_gradient = -(1/len(x)) * np.sum(error)
theta1_gradient = -(1/len(x)) * np.sum(error * x)
theta0 = theta0 - alpha * theta0_gradient
theta1 = theta1 - alpha * theta1_gradient
print("Theta0:", theta0)
print("Theta1:", theta1)
Scikit Learn 패키지로 Linear Regression 모델 적용하기
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Generate random data for the regression
np.random.seed(0)
x = 2 - 3 * np.random.normal(0, 1, 20)
y = x - 2 * (x ** 2) + 0.5 * (x ** 3) + np.random.normal(-3, 3, 20)
# Reshape the data for the scikit-learn API
x = x.reshape(-1, 1)
y = y.reshape(-1, 1)
# Train the linear regression model
model = LinearRegression()
model.fit(x, y)
# Predict using the trained model
y_pred = model.predict(x)
# Visualize the results
plt.scatter(x, y, color='blue')
plt.plot(x, y_pred, color='red')
plt.title("Linear Regression using scikit-learn")
plt.xlabel("Independent Variable (x)")
plt.ylabel("Dependent Variable (y)")
plt.show()
이 포스팅에서는 Linear Regression이 무엇인지, Linear Regression 모델의 Cost Function은 무엇인지, 또 최적화하는 방식과 Gradient Descent 알고리즘이 어떻게 최적화해나가는지에 대해 알아보았습니다. 또 Scikit learn 패키지를 활용하여 파이썬으로 Linear Regression을 적용하는 방식에 대해서도 코드예제와 함께 알아보았습니다. (참고 포스팅: 머신러닝 Overfitting 이해하기)
'머신러닝' 카테고리의 다른 글
| Logistic Regression 이해하기 : Sigmoid 함수, ROC 커브, Threshold 찾기 (0) | 2023.02.13 |
|---|---|
| 머신러닝 Accuracy, Precision, Recall, F1-Score, Confusion Matrix 이해하기 (0) | 2023.02.13 |
| 챗 GPT로 머신러닝 코딩 하기(파이썬) (0) | 2023.02.12 |
| 머신러닝 오버피팅 (Overfitting) 이해하기, 원인과 방지 방법, 언더피팅(underfitting)과 차이점 등 (0) | 2023.02.11 |
| 머신러닝 Cross-Validation 이란? (0) | 2023.02.10 |




댓글